Introduction
A treap is a randomized binary search tree. A node in a key has following two information in addition to usual pointers.
- key: This is a normal key as in other binary search trees.
- priority: This is the priority of the node. The priority must be a random real number (or a random integer).
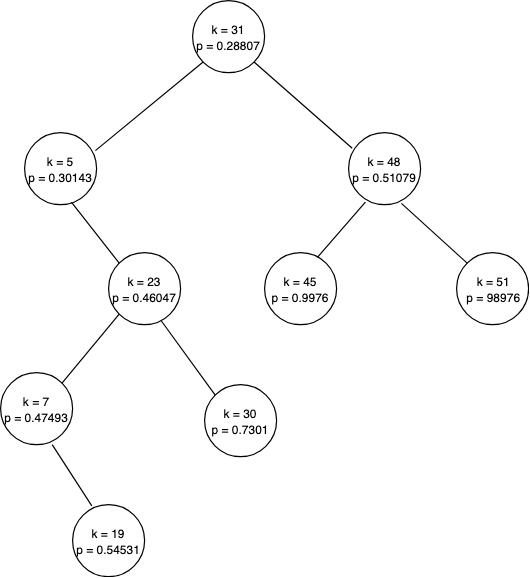
A treap is a binary search tree as well as a binary heap at the same time. It is a binary search tree by key and a heap by priority. Figure 1 depicts a treap.
If you consider the keys (denoted by k in the figure) only, the tree is a binary search tree. That means keys of the left subtree is less than or equal to the key of the node and the keys of the right subtree is greater than or equal to the key of the node. Likewise, if you consider the priorities (denoted by p in the figure) only, the tree is a min-heap (you can also use max-heap). Which means the priority of a parent node is smaller than the priorities of its child nodes.
Why treap?
When we have a sequence of items available, we can randomly permute the items and insert them into the tree one by one. This creates a balanced binary search tree with high probability as discussed here. But what if we do not have all the items at once? If we receive the items one at a time, we cannot build the random binary search tree by inserting the item as they come into the tree. For this, we need treap.
Operations
We discuss insert and delete operation here. Other operations are same as the operations in the ordinary binary search tree. We also discuss two auxiliary operations called split and merge.
Insertion
We insert a node $x$ in the treap $T$ using the following process.
- Create a node $x$ with a key and a random priority. Insert $x$ in the tree using an ordinary binary search tree insert operation.
- Move $x$ up in the tree using tree rotations. We move $x$ until its priority is less than its parent’s priority.
To move $x$ up in the tree we examine whether $x$ is a left or a right child. If it is a left child, we perform right rotation otherwise we perform the left rotation at $x$’s parent node. The insertion operation is illustrated in Figure 2.
The pseudo code of the insert operation is given below.
TREAP-INSERT(T, x)
BST-INSERT(T, x)
MOVE-UP(x)
The pseudo code of MOVE-UP method is as follows
MOVE-UP(x)
if x.parent == NIL
return
if x.parent $\ne$ NIL and x.priority $\ge$ x.parent.prority
return
if x == x.parent.left
RIGHT-ROTATE(x.parent)
else LEFT-ROTATE(x.parent)
MOVE-UP(x)
Deletion
To delete a node with key $k$ from the treap $T$, we perform the opposite of the insertion operation as follows
- Find the node $x$ with key $k$.
- Move $x$ down the tree until it becomes a leaf node.
- Chop off $x$ from the tree.
To move down $x$ in the tree, we perform a left or a right rotation at $x$. The pseudo code for the delete operation is given below.
TREAP-DELETE(T, k)
x = BST-FIND(T, k)
MOVE-DOWN(x)
if x == x.parent.left
x.parent.left = NIL
else x.parent.right = NIL
The pseudo code of MOVE-DOWN is as follows.
MOVE-DOWN(x)
if x.left == NIL and x.right == NIL
return
if x.left $\ne$ NIL and x.right $\ne$ NIL
if x.left.priority $<$ x.right.priority
RIGHT-ROTATE(x)
else LEFT-ROTATE(x)
else if x.left $\ne$ NIL
RIGHT-ROTATE(x)
else LEFT-ROTATE(x)
MOVE-DOWN(x)
Split
The split operation divides the tree into two trees $L$ and $R$ along some pivot key $P$, so that all the nodes in $L$ have keys less than $P$ and all the nodes in $R$ have keys bigger than $P$. $L$ and $R$ themselves must be the valid treaps. To split a treap $T$, we do the following.
- Create a node $x$ with key $P$ and priority $-\infty$.
- Insert $x$ into the tree. Since $x$ has the smallest priority, the insert operation moves $x$ to the root of the tree.
- Chop off $x$ from the tree. The left subtree of $x$ is $L$ and the right subtree of $x$ is $R$.
The pseudo code for split operation can be written as follows. (we assume that $x$ has key $P$ and priority $-\infty$ before calling TREAP-SPLIT).
TREAP-SPLIT(T, L, R, x)
TREAP-INSERT(T, x)
L.root = T.root.left
R.root = T.root.right
T.root.left = NIL
T.root.right = NIL
Merge
We merge operation joins two treaps $L$ and $R$, where every node in $L$ has a smaller search key than any node in $R$, into one super-treap $T$. To merge $L$ and $R$, we do the following
- Create a dummy node $x$ and make $L$ its left subtree and $R$ its right subtree.
- Move $x$ down the tree until it becomes a leaf node.
- Chop it off.
The pseudo code for merge operation is as follows.
MERGE(T, L, R)
largest = L.MAXIMUM(L.root)
smallest = R.MINIMUM(R.root)
// create a dummy node with $\infty$ priority
x = new NODE((largest.key + smallest.key)/2, $\infty$)
x.left = L.root
x.right = R.root
MOVE-DOWN(x)
if x == x.parent.left
x.parent.left = NIL
else x.parent.right = NIL
Complexity Analysis
Since treap is a randomized binary search tree, we compute the expected running time of the operation. It turns out that every search, insertion, deletion, split, and join operation in an $n$-node randomized binary search tree takes $O(\log n)$ expected time. If you are interested in the actual computation of this expected time, you can see it here.
Implementation
I have implemented the treap data structure in C++. You can find the source code on GitHub (link). Please note that I haven’t tested the code thoroughly and some corner cases are not tested. Do not use this code in the production. Use it for educational propose only.