Introduction
A 2-3 tree is a tree where a node can have 2 or 3 children nodes. A node with 2 children has one key (data) on it and we call it a 2-node whereas a node with 3 children has two keys on it and we call it a 3-node. Figure 1 shows an example of a 2-node and a 3-node.
Just like a node in a binary search tree, in a 2-node, the keys of a left child node must be less than or equal to the key of a parent node and the keys of the right child node must be greater than or equal to the key of the parent node. In case of a 3-node, the keys of the left child node must be less than or equal the left key of the parent node, the keys of the middle child node must be in between the middle key of the parent node, and the keys of the right child node must be greater than or equal to the right key of the parent node. An example of a 2-3 tree is given in Figure 2.
A 2-3 tree maintains the following 2 properties.
- Perfect balance: Every path from the root to the leaf node has the same length.
- Symmetric order: In order traversal yields keys in ascending order (just like a binary search tree).
What is the height of the tree
We know that the height of the tree directly impacts the running time. Since the 2-3 has both 2-node and 3-node, the hight of the tree (h) varies as follows.
h = $\log_2(n)$ if all nodes are 2-node. (Worst case)
h = $\log_3(n)$ if all the nodes are 3-node. (Best case)
This means the height of the tree is in between $\log_2(n)$ and $\log_3(n)$.
The search operation
The search operation on a 2-3 tree is similar to the search operation on a binary search tree. The only difference is when dealing with the 3-node. If we are searching for a key k and we are on a 3-node with keys a and b, we do the following.
- If
kis equal to any one of the keys, we stop. - If
kis smaller thana, we continue the search operation towards a left child. - If
kis in betweenaandb, we continue the search operation towards a middle child. - If
kis larger thanb, we continue the search operation towards a right child.
The insertion operation
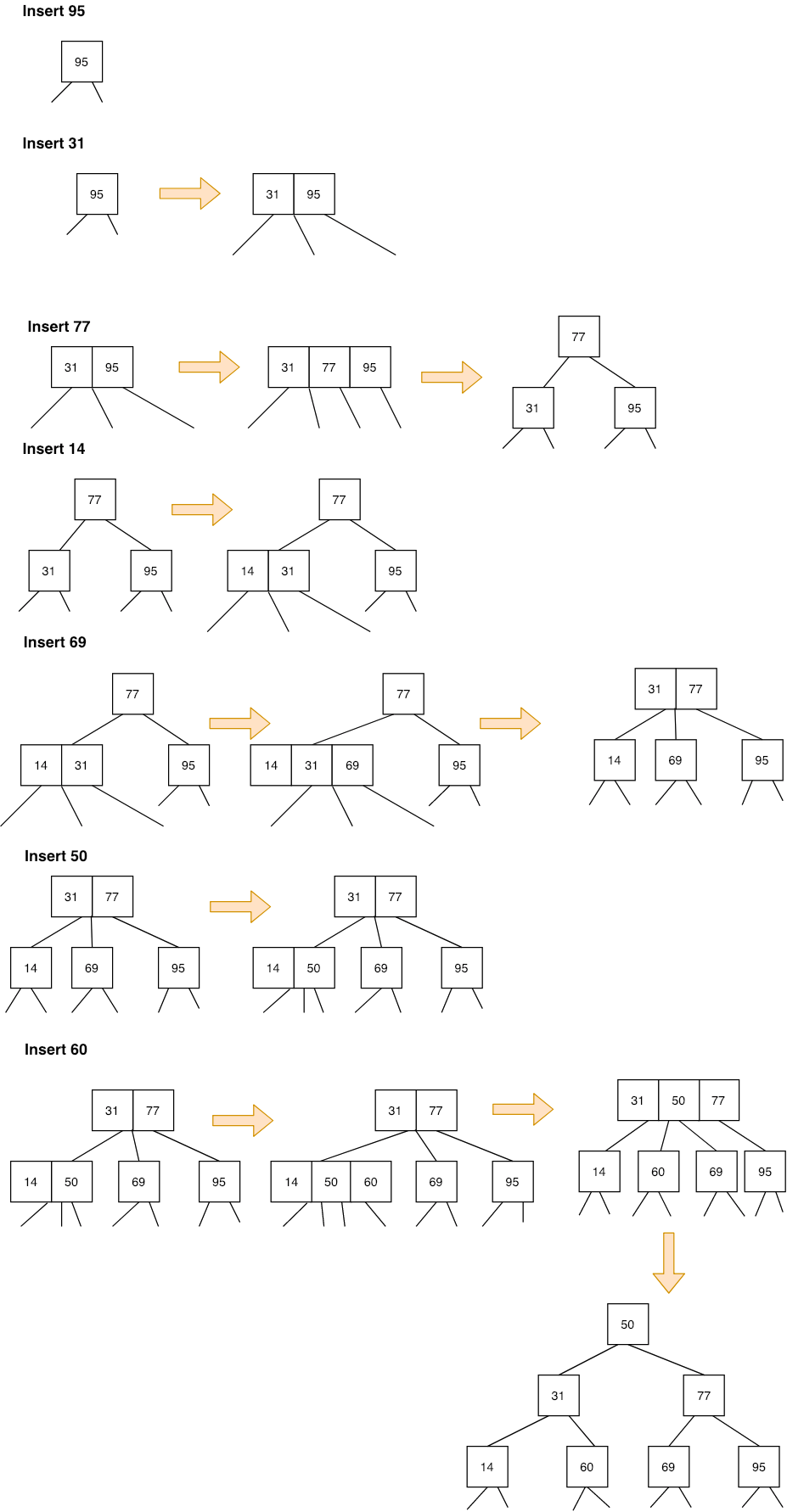
The insertion operation in a 2-3 is a little bit tricky. The insertion operation must make sure that the tree remains perfectly balance after the insertion. To insert a node $N$ in a 2-3 tree $T$, we need to consider 2 cases as follows.
- If the tree is
null, we make $N$ the root of the tree $T$. - Otherwise, search the tree unless we reach a leaf node where we need to insert it. In this case, we need to consider further 2 cases.
a. If the leaf node is a 2-node, make it a 3-node. This is illustrated in Figure 3.
b. If the leaf node is a 3-node then (a) make it a temporary 4-node (b) split the 4-node and make the middle key the parent of the other two keys. The left key becomes the left child and the right becomes the right child. This is illustrated in Figure 4.
Figure 5 illustrates the insert operation.
Implementation
The implementation of a 2-3 tree is not straightforward. Due to its two kinds of nodes, it makes much more difficult to implement 2-3 tree than any other binary search trees. Even though we can implement a 2-3 tree, we go for a much better version of it. That means, we convert the 2-3 tree into a Red-Black tree and implement it.
Mapping 2-3 tree to Red-Black tree.
The process for converting 2-3 tree to a left leaning Red-Black tree is given below.
- A 2-node becomes a new Black node.
- We split the 3-node into two 2-nodes and insert a link between them. We move down the left node making the link left lean.
- The left node (which was moved down) becomes the new Red node and the right nodes become the new Black node.
Let me illustrate steps 2 and 3 with an example.
When converting a 2-3 tree to a Red-Black tree, we make the following observation.
- Every node is either red or black.
- The root is always black.
- A red node cannot have a red child node.
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
A complete mapping from a 2-3 tree to an RB tree is illustrated in Figure 7.